Today I want to share another example of how money isn’t math and math isn’t money by demonstrating the concepts of average rate of return on an investment and the actual rate of return.
Assume you have $100,000 and you have two investment options to choose from and both offered an average rate of return of 5.03%. Which would you choose?
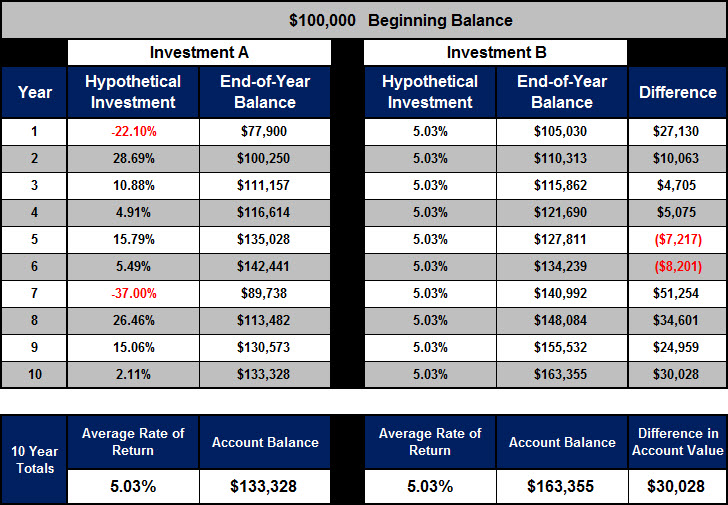
Let’s evaluate each investment individually.
In year one, Investment A lost 22.10% and your account balance fell from $100,000 to $77,900. From year two to year six, Investment A bounced back and showed gains of 28.69%, 10.88%, 4.91%, 15.79%, and 5.49%. Your account balance grew from $77,900 to $142,441. Then, in year seven, Investment A lost 37.00% and your account balance fell to $89,738. From year eight to year ten, Investment A bounced back with returns of 26.46%, 15.06%, and 2.11% and increased your account balance to $133,328. Over the 10 year investment period your average rate of return was 5.03%.
Looking closely at Investment B, your annual rate of return was a consistent 5.03% and your account balance grew every year and ended up at $163,355 from the $100,000 you started with. Over the 10 year investment period your average rate of return was 5.03%.
Comparing the two investments you can see that the math shows both investments had an average rate of return of 5.03%. However, the money shows they have different account values. If the average rates of return are the same, how is it that the accounts have different account values? That is because the actual rate of return is different than the average rate of return. Investment A had an actual rate of return of 2.92% over the 10 year period and Investment B had an actual rate of return of 5.03% over the 10 year period.
Which investment would make you feel more comfortable? Which investment would provide you with more peace of mind? Which investments performance most closely resembles your current portfolio?
Key Understanding: Compounding and consistency are the keys to growth.
Investment B demonstrates the power of compounding and consistency, while Investment A demonstrates the challenges of inconsistency in rates of return. The account value of Investment A is $30,028 less than that of Investment B, which is an overall loss of approximately 18% of the total gains.
Averages lie! Averages misrepresent the facts. The use of averages can make losses seem less significant than they really are and are powerful tools to promote popular concepts like dollar cost averaging, asset allocation, diversification, buy and hold, etc…
While achieving a consistent rate of return year-in and year-out is a worthy pursuit, what if you could simply eliminate the losses? Is that even possible? If eliminating the losses were possible when would you want to know?
If you’re interested in learning more about how to eliminate the losses in your financial profile please contact us to schedule a time to talk.
Leave a Comment